EJEMPLO DE BINOMIO
Se denomionan binomios a las actividades efectuadas en álgebra conformadas únicamente por dos palabras separadas por un carácter de suma (+) o de resta (-).
Lo citado anteriormente nos viene a demostrar que los binomios son una ejecución algebraica la cual la forman la suma de dos monomios.
Para efectuar una ejecución de disinución de conclusiones similares en binomios, es imprescindible realizar la suma de los coeficientes de las conclusiones que poseen literales similares elevada a la misma potencia.
Se dan binomios que poseen particularidades determiandas, entre los que podemos destacar los binomios de diferencia de cuadrados, o el binomio de Newton.
Un binomio es una expresión algebraica compuesta por dos términos. En la siguiente figura se presenta un ejemplo de binomio.
El cuadrado de un binomio es el producto de multiplicar el binomio por si mismo, en la siguiente figura lo podemos observar.
Coeficiente Binomial
Determina una relación entre los números naturales n y k, con k "menor o igual que n"

Se utiliza para determinar el coeficiente de un Binomio de potencia "n" En Ia posición k-1
¿Qué es un binomio con término común?
Son las multiplicaciones de binomios con expresiones algebraicas que tienen en común un término o una literal.
Ejemplo: (a+1) (a-1)
El termino común de estos binomios es a
Bínomío Cuadrado Perfecto
Los binomios cuadrados perfectos son de la forma
(a+b)2=(a+b)*(a+b)=a2+20b+b2.
Realizando la multiplicación de forma algebraica podemos comprobar que el resultado sea correcto.
Veamos algunos ejemplos.
Ejemplo 1 : Desarrollar (x+4)2
Fórmula: cuadrado del primer rérmino + el doble productro del primero por el segundo + cuadrado del segundo.
Cuadrado del primer término = x2 , doble producto del primero por el segundo =(2x)(4)= 8x ,cuadrado del
primero por el segundo =(2x)(4)= 8x ,cuadrado del segundo trérmino : (4 al cuadrado)= 16
De esta forma: (x+4)2= x2+8x+16.
Regla del cuadrado de un binomio
El cuadrado de un binomio es uno de los casos más sencillos cuando elevamos un binomio a una potencia .Para estos casos, son conocidas las fórmulas "el cuadrado del primero más [o menos] el doble del primero por el segundo más el cuadrado del segundo.
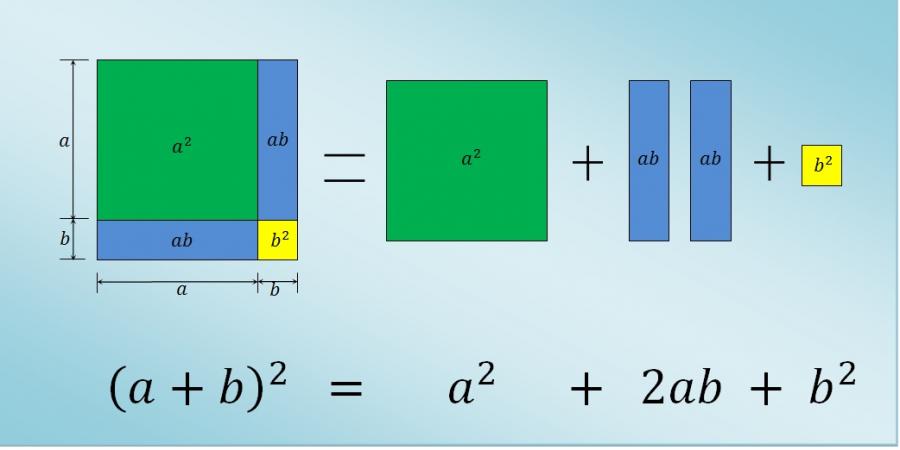
Esta es la demostración de la regla del cuadrado de un binomio. La cual dice que el cuadrado de binomio es el primer término elevado al cuadrado más dos veces el segundo por el primero mas el segundo termino elevado al cuadrado.
(a+b)2 = a2 + 2ab + b2
|

